Câu số 1:   Trong các mệnh đề sau, mệnh đề nào đúng?

Câu số 2:  

Cắt hình nón đỉnh $S$ bởi mặt phẳng đi qua trục ta được một tam giác vuông cân, cạnh huyền bằng

$a\sqrt2$. Thể tích khối nón là:

Câu số 3:   Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $AB=a\sqrt3, BC=a\sqrt2$. Cạnh bên $SA=a$ và $SA$ vuông góc với mặt phẳng đáy. Khoảng cách giữa $SB$ và $DC$ bằng:

Câu số 4:   Cho khối chóp có đáy là hình vuông cạnh $𝑎$ và chiều cao bằng $2𝑎$. Thể tích của khối chóp đã cho bằng

Câu số 5:  

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, $SA$ vuông góc với đáy và $SA=2a$. Gọi $M$ là trung điểm của $SD$. Tính khoảng cách $d$ giữa đường thẳng $SB$ và mặt phẳng $ACM$.

Câu số 6:   Trong không gian $𝑂𝑥𝑦𝑧$, cho mặt cầu $(𝑆): (𝑥 + 1)^2 + (𝑦 + 1)^2 + (𝑧 + 1)^2 = 9$ và điểm $𝐴(2; 3; − 1)$. Xét các điểm $𝑀$ thuộc $(𝑆)$ sao cho đường thẳng $𝐴𝑀$ tiếp xúc với $(𝑆), 𝑀$ luôn thuộc mặt phẳng có phương trình là

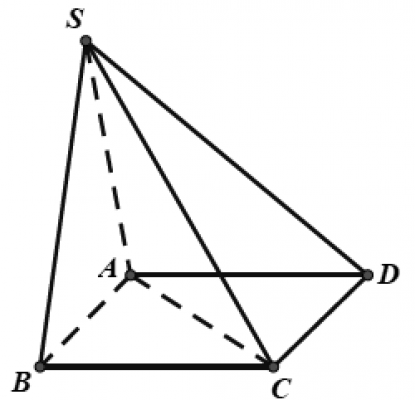
Câu số 7:   Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$, mặt bên $SAB$ là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (minh họa như hình vẽ bên). Khoảng cách từ $D$ đến mặt phẳng $(SAC)$ bằng

Câu số 8:   Trong không gian $Oxyz$, hình chiếu vuông góc của điểm $M(2;1;-1)$ trên trục $Oy$ có tọa độ là

Câu số 9:   Cho hai mặt phẳng $(P), (Q)$, cắt nhau theo giao tuyến là đường thẳng $d$. Đường thẳng a song song với cả hai mặt phẳng $(P), (Q)$. Khẳng định nào sau đây đúng

Câu số 10:  

Cho đường thẳng $d_2$ cố định, đường thẳng $d_1$ song song và cách $d_2$ một khoảng cách không đổi. Khi $d_1$ quay quanh $d_2$ ta được