Câu số 11:  

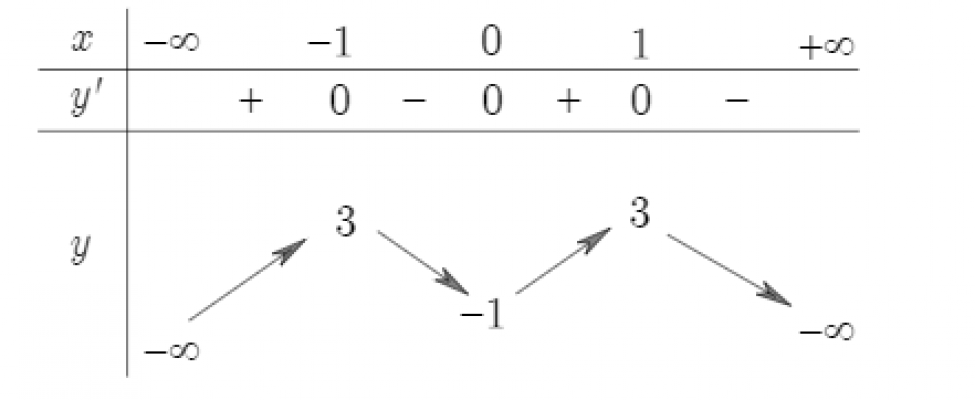
Cho hàm số $y = f(x)$ xác định, liên tục trên $R$ và có bảng biến thiên như hình bên. Đồ thị hàm số $y = f(x)$ cắt đường thẳng $x = -2018$ tại bao nhiêu điểm?

Câu số 12:  

Trong không gian Oxyz một véctơ pháp tuyến của mặt phẳng $(a): x - 2y + 3z + 1 = 0$ là

Câu số 13:  

Trong không gian $Oxyz$ cho hai điểm $M(1; 1; 0)$ và $N(3; 3; 6)$. Mặt phẳng trung trực của đoạn thẳng $MN$ có phương trình là

Câu số 14:  

Phương trình $\ln\left ( x -\frac{1}{2} \right )$$\ln\left ( x + \frac{1}{2} \right)$$\ln\left ( x + \frac{1}{4} \right )$$\ln\left ( x + \frac{1}{8} \right ) = 0$ có bao nhiêu nghiệm?

Câu số 15:  

Cho hình phẳng $(D )$ được giới hạn bởi các đường $x = 0, x = \pi$, $y = 0, y = -\sin x$. Thể tích $V$ của khối tròn xoay tạo thành khi quay $(D )$ xung quanh trục $Ox$ được tính theo công thức

Câu số 16:  

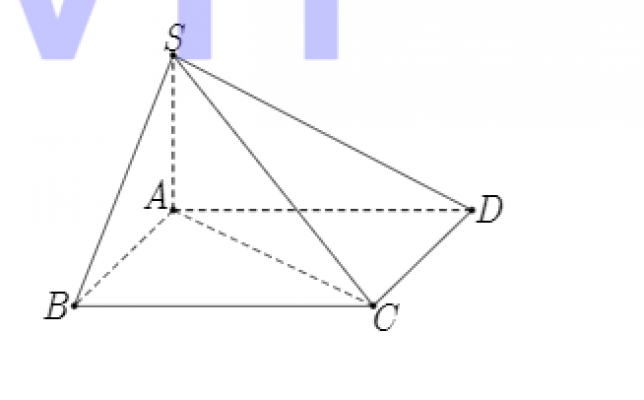
Cho hình chóp $S ABCD$ có đáy $ABCD$ là hình chữ nhật, cạnh $AB = a, AD = \sqrt{3}a$. Cạnh bên $SA = \sqrt{2}a$ và vuông góc với mặt phẳng đáy. Góc giữa đường thẳng $SB$ và mặt phẳng $(SAC )$ bằng:

Câu số 17:  

Đạo hàm của hàm số $y = \left (x^{2} + x + 1 \right )^{\frac{1}{2} }$ là

Câu số 18:  

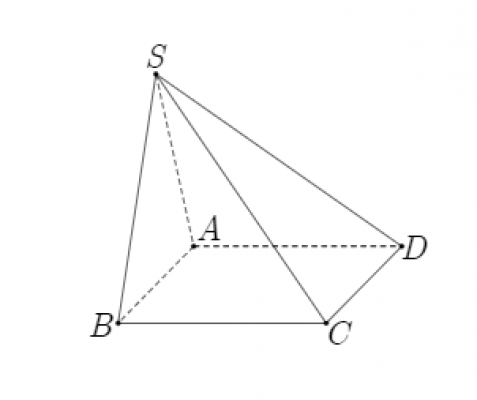
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2 a cạnh bên SA = $\sqrt{5}a$ mặt bên SAB là tam giác cân đỉnh S và thuộc mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng AD và SC bằng

Câu số 19:  

Trong không gian Oxyz cho điểm A(- 1; 1; 6) và đường thẳng $$\Delta : \left\{\begin{matrix} x = 2 + t \\ y = 1 - 2t \\ z = 2t\end{matrix}\right.$$ Hình chiếu vuông góc của điểm A trên đường thẳng D là

Câu số 20:  

Cho các số phức $z_{1} = 3 + 2i$ , $z_{2} = 3 - 2i$ Phương trình bậc hai có hai nghiệm $z_{1} $ và $z_{2}$ là