Câu số 31:
Giả sử $F(x)$ là một nguyên hàm của $ f(x) = \frac{\ln(x+3)}{x^{2} } $ sao cho $F(-2) + F(1) = 0$. Giá trị của $F(-1) + F(2)$ bằng
Câu số 32:
Cho hình chóp tam giác đều S.ABC có cạnh AB bằng a góc tạo bởi hai mặt phẳng (SAB) và (ABC) bằng $ 60^{\circ}$. Diện tích xung quanh của hình nón đỉnh S và có đường tròn đáy ngoại tiếp tam giác ABC bằng
Câu số 33:
Trong không gian ,Oxyz cho điểm A(1; 2; -1), đường thẳng $d:\frac{x - 1}{2}=\frac{y + 1}{1} = \frac{z - 2}{-1}$ và mặt phẳng (P): x + y + 2z + 1 = 0. Điểm B thuộc mặt phẳng (P) thỏa mãn đường thẳng AB vuông góc và cắt đường thẳng d. Tọa độ điểm B là
Câu số 34:
Cho các hàm số f(x) và g(x) liên tục trên mỗi khoảng xác định của chúng và có bảng biến thiên được cho như hình vẽ dưới đây. Mệnh đề nào sau đây sai?

Câu số 35:
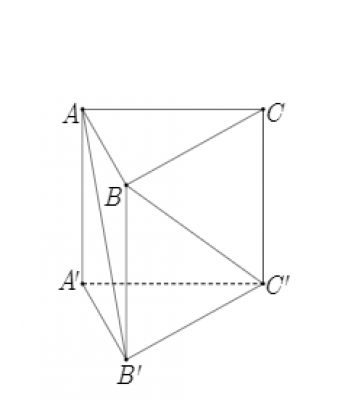
Cho hình lăng trụ tam giác đều $ABC.{A}'{B}'{C}'$ có AB = a và $A{A}' = \sqrt{2}a$. Góc giữa hai đường thẳng AB¢ và BC¢ bằng
Câu số 36:
Trong không gian Oxyz, cho mặt cầu $(S): (x-1)^{2} + (y - 2)^{2} + (z + 1)^{2} = 6$ tiếp xúc với hai mặt phẳng (P): x + y + 2z + 5 = 0 và (Q): 2x - y + z - 5 = 0 lần lượt tại các tiếp điểm A, B Độ dài đoạn thẳng AB là
Câu số 37:
Trong không gian $Oxyz$ cho hai đường thẳng d: $ \left\{\begin{matrix} x = 1 + t& & & & \\ y = 2 - t& & & & \\ z = t& & & &\end{matrix}\right.$ d’: $ \left\{\begin{matrix} x = 2{t}'& & & & \\ y = 1 + {t}'& & & & \\ z = 2 + {t}'& & & &\end{matrix}\right.$ Đường thẳng D cắt $d$, $d'$ lần lượt tại các điểm A, B thỏa mãn độ dài đoạn thẳng AB nhỏ nhất. Phương trình đường thẳng D là
Câu số 38:
Trong không gian Oxyz, cho đường thẳng $ d: \frac{x - 1}{1} = \frac{y + 1}{1}=\frac{z - m}{2}$ và mặt cầu $ (S): (x - 1)^{2} + y - 1^{2} + (z - 2)^{2} = 9$ . Tìm m để đường thẳng d cắt mặt cầu (S) tại hai điểm phân biệt E,F sao cho độ dài đoạn thẳng EF lớn nhất
Câu số 39:
Biết rằng giá trị nhỏ nhất của hàm số $y = mx + \frac{36}{x + 1}$ trên [0; 3] bằng 20. Mệnh đề nào sau đây đúng?
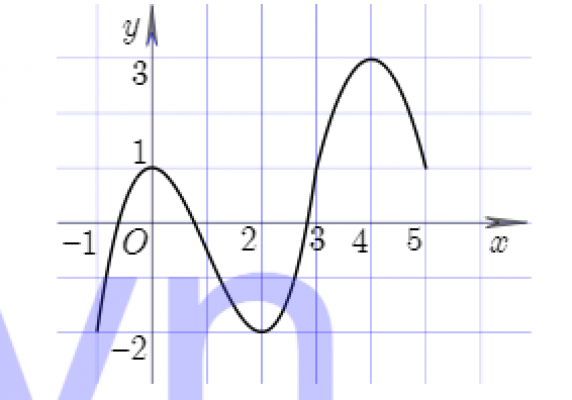
Câu số 40:
Cho hàm số y = f(x) có đồ thị của hàm số $y = {f}'(x)$ được cho như hình bên. Hàm số $y = -2f(2-x) + x^{2}$ nghịch biến trên khoảng