Câu số 11:  

Tiếp tuyến của đồ thị hàm số $y = \frac{x^{3} }{3}-2x^{2}+3x+1$ song song với đường thẳng y = 3x + 1 có phương trình là

Câu số 12:  

Cho các số thực dương a,b,c với $c\neq 1$ . Khẳng định nào sau đây là sai?

Câu số 13:  

Giá trị nhỏ nhất của hàm số $y = \frac{x^{2}+3}{x +1}$ trên đoạn [-4;-2] là

Câu số 14:  

Gọi r là bán kính đường tròn đáy và l là độ dài đường sinh của hình trụ. Diện tích xung quanh của hình trụ là:

Câu số 15:  

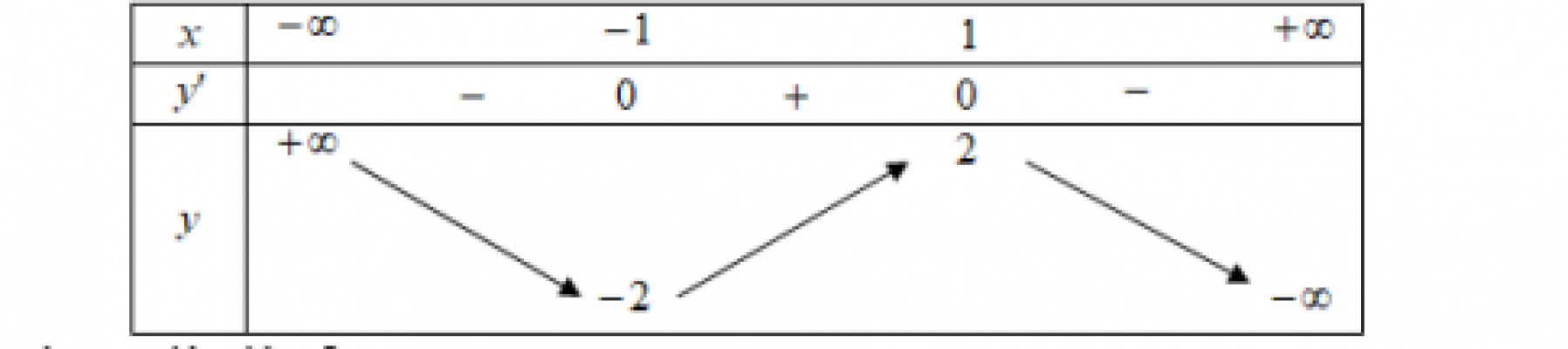
Cho hàm số y = f(x) xác định, liên tục trên $\mathbb{R}$ và có bảng biến thiên. Khẳng định nào sau đây đúng?

Câu số 16:  

cho hai số phức $z_{1} = 2 + 3i, z_{2} = 1 + i$. Giá trị của biểu thức $\left | z_{1}+3z_{2} \right |$ là

Câu số 17:  

Gọi là nghiệm phức có phần ảo dương của phương trình $z^{2}+2z+10=0$. Tính $iz_{0}$

Câu số 18:  

Các khoảng đồng biến của hàm số $y = x^{4}-8x^{2}-4$ là

Câu số 19:  

Trong không gian Oxyz, cho điểm A(1;-2;3). HÌnh chiếu vuông góc của điểm A trên mặt phẳng (Oxy) là điểm M có tọa độ:

Câu số 20:  

Cho số phức thỏa mãn $\left | z - 1 \right | = \left | z - 2 + 3i \right |$. Tập hợp các điểm biểu diện số phức z là