Câu số 31:   Ông A dự định sử dụng hết 6, 5 $m^2$ kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?

Câu số 32:   Một chất điểm $𝐴$ xuất phát từ $𝑂$, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật$v(t)=\frac{1}{180} t^2 + \frac{11}{18}t$ (m/s), trong đó $t$ (giây) là khoảng thời gian tính từ lúc bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm 𝐵 cũng xuất phát từ 𝑂, chuyển động thẳng cùng hướng với $𝐴$ nhưng chậm hơn 5 giây so với $𝐴$ và có gia tốc bằng $𝑎$ ($m/s^2$) ( là hằng số). Sau khi $B$ xuất phát được 10 giây thì đuổi kịp $𝐴$. Vận tốc của $B$ tại thời điểm đuổi kịp $𝐴$ bằng

Câu số 33:   Trong không gian $𝑂𝑥𝑦𝑧$, cho điểm $𝐴(1; 2; 3)$ và đường thẳng $d:\frac{x-3}{2} = \frac{y-1}{1} = \frac{z+7}{-2}$. Đường thẳng đi qua $𝐴$, vuông góc với $𝑑$ và cắt trục $𝑂𝑥$ có phương trình là

Câu số 34:   Gọi $S$ là tập hợp tất cả các giá trị nguyên của tham số sao $𝑚$ cho phương trình $16^x-m.4^{x+1}+5m^2-45=0$ có hai nghiệm phân biệt. Hỏi $S$ có bao nhiêu phần tử?

Câu số 35:   Có bao nhiêu giá trị nguyên của tham số $𝑚$ để hàm số $y=\frac{x+2}{x+5m}$ đồng biến trên khoảng $(-\infty;-10)$?

Câu số 36:   Có bao nhiêu giá trị nguyên của tham số $𝑚$ để hàm số $𝑦 = x^8 + (𝑚 − 2)x^5 − (m^2 − 4)x^4 + 1$ đạt cực tiểu tại $𝑥 = 0$?

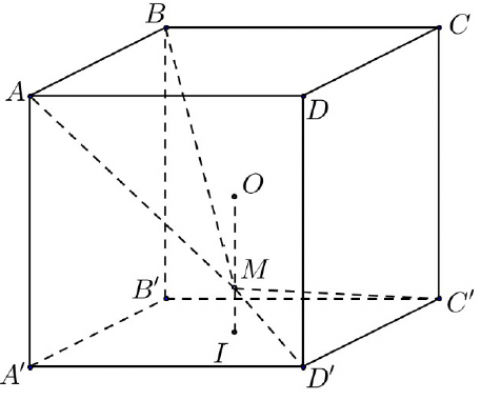
Câu số 37:   Cho hình lập phương $𝐴𝐵𝐶𝐷. 𝐴'𝐵'𝐶'𝐷'$ có tâm $𝑂$. Gọi $𝐼$ là tâm của hình vuông $𝐴'𝐵'𝐶'𝐷'$ và $𝑀$ là điểm thuộc đoạn thẳng $𝑂𝐼$ sao cho $𝑀𝑂 = 2𝑀𝐼$ (tham khảo hình vẽ). Khi đó côsin của góc tạo bởi hai mặt phẳng $(𝑀𝐶'𝐷')$ và $(𝑀𝐴𝐵)$ bằng

Câu số 38:   Có bao nhiêu số phức $𝑧$ thỏa mãn $|𝑧|(𝑧 − 4 − 𝑖) + 2𝑖 = (5 − 𝑖)𝑧$?

Câu số 39:   Trong không gian $𝑂𝑥𝑦𝑧$, cho mặt cầu $(𝑆): (𝑥 + 1)^2 + (𝑦 + 1)^2 + (𝑧 + 1)^2 = 9$ và điểm $𝐴(2; 3; − 1)$. Xét các điểm $𝑀$ thuộc $(𝑆)$ sao cho đường thẳng $𝐴𝑀$ tiếp xúc với $(𝑆), 𝑀$ luôn thuộc mặt phẳng có phương trình là

Câu số 40:   Cho hàm số $y=\frac 1 4 x^4 - \frac 7 2 x^2$ có đồ thị $(C)$. Có bao nhiêu điểm $A$ thuộc $(C)$ sao cho tiếp tuyến của $(𝐶)$ tại $𝐴$ cắt $(𝐶)$ tại hai điểm phân biệt $M(x_1;y_1),N(x_2;y_2)$ ($M,N$ khác $A$) thỏa mãn $y_1-y_2=6(x_1-x_2)$)?