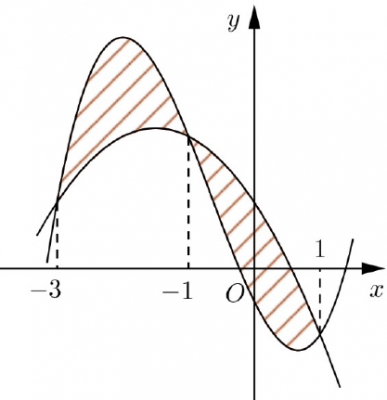
Câu số 41:   Cho hai hàm số $𝑓(𝑥) = ax^3+bx^2+ 𝑐𝑥 −\frac 1 2$ và $𝑔(𝑥) = dx^2 + 𝑒𝑥 + 1$ $(𝑎, 𝑏, 𝑐, 𝑑, 𝑒 \in \mathbb R)$. Biết rằng đồ thị của hàm số $𝑦 = 𝑓(𝑥)$ và $𝑦 = 𝑔(𝑥)$ cắt nhau tại ba điểm có hoành độ lần lượt là $−3; − 1; 1$ (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng

Câu số 42:   Cho khối lăng trụ $𝐴𝐵𝐶.𝐴'𝐵'𝐶'$, khoảng cách từ $𝐶$ đến đường thẳng $𝐵𝐵'$ bằng 2, khoảng cách từ $𝐴$ đến các đường thẳng $𝐵𝐵'$ và $𝐶𝐶'$ lần lượt bằng 1 và $\sqrt3$, hình chiếu vuông góc của $𝐴$ lên mặt phẳng $(𝐴'𝐵'𝐶')$ là trung điểm $𝑀$ của $𝐵'𝐶'$ và $𝐴'𝑀 = =\frac {2\sqrt3}3$. Thể tích của khối lăng trụ đã cho bằng

Câu số 43:   Ba bạn A, B, C mỗi bạn viết ngẫu nhiên lên bảng một số tự nhiên thuộc đoạn [1;17]. Xác suất để ba số được viết ra có tổng chia hết cho 3 bằng

Câu số 44:   Cho $𝑎 > 0, 𝑏 > 0$ thỏa mãn $$\log_{3a+2b+1} (9a^2 + b^2 + 1) + \log_{6ab+1} (3𝑎 + 2𝑏 + 1) = 2$$ Giá trị của $𝑎 + 2𝑏$ bằng

Câu số 45:   Cho hàm số $𝑦 = \frac {𝑥 − 1}{𝑥 + 2}$ có đồ thị $(C)$. Gọi $I$ là giao điểm của hai tiệm cận của $(C)$ Xét tam giác đều $𝐴𝐵𝐼$ có hai đỉnh $𝐴, 𝐵$ thuộc $(𝐶)$, đoạn thẳng $𝐴𝐵$ có độ dài bằng

Câu số 46:   Cho phương trình $5^x + 𝑚 = \log^5 (𝑥 − 𝑚)$ với $m$ là tham số. Có bao nhiêu giá trị nguyên của $𝑚 \in (−20; 20)$ để phương trình đã cho có nghiệm ?

Câu số 47:   Trong không gian $𝑂𝑥𝑦𝑧$, cho mặt cầu $(𝑆)$ có tâm $𝐼(−2; 1; 2)$ và đi qua điểm $𝐴(1; − 2; − 1)$. Xét các điểm $𝐵, 𝐶, 𝐷$ thuộc $(𝑆)$ sao cho $𝐴𝐵, 𝐴𝐶, 𝐴𝐷$ đôi một vuông góc với nhau. Thể tích của khối tứ diện $𝐴𝐵𝐶𝐷$ có giá trị lớn nhất bằng

Câu số 48:   Cho hàm số $𝑓(𝑥)$ thỏa mãn $𝑓(2) = −\frac 2 9$ và $f'(x)=2x[f(x)]^2$ với mọi $x\in \mathbb R$. Giá trị của $𝑓(1)$ bằng

Câu số 49:   Trong không gian $𝑂𝑥𝑦𝑧$, cho đường thẳng $$\left\{\begin{array}{l} x=1+3t \newline y=1+4t \newline z=1 \end{array}\right.$$ Gọi $\Delta$ là đường thẳng đi qua điểm $𝐴(1; 1; 1)$ và có vectơ chỉ phương $\vec u=(1; − 2; 2)$. Đường phân giác của góc nhọn tạo bởi $d$ và $\Delta$ có phương trình là

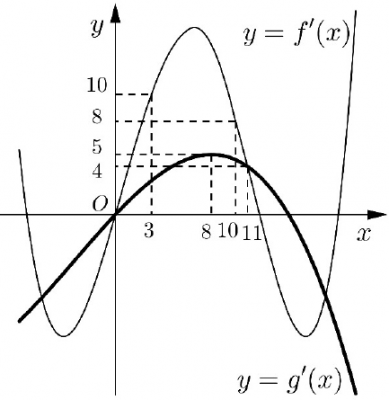
Câu số 50:   Cho hai hàm số $𝑦 = 𝑓(𝑥), 𝑦 = 𝑔(𝑥)$. Hai hàm số $𝑦 = 𝑓'(x)$ và $𝑦 = g'(𝑥)$ có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số $𝑦 = g'(𝑥)$. Hàm số $ℎ(𝑥) = 𝑓(𝑥 + 4) − g(2𝑥 −\frac 3 2)$ đồng biến trên khoảng nào dưới đây?