Câu số 41:
Cho tham số thực $m$, biết rằng phương trình 4 $^{x}-(m+4) 2^{x}+2=0$ có hai nghiệm thực $x_{1} ; x_{2}$ thỏa mãn $\left(x_{1}+2\right)\left(x_{2}+2\right)=4$ . Giá trị của $m$ thuộc khoảng nào dưới đây ?
Câu số 42:
Trong không gian Oxy $z$, cho các điểm $A(1 ; 0 ; 0), B(3 ; 2 ; 4)$ và $C(0 ; 5 ; 4) .$ Xét diễm $M(a ; b ; c)$ thuộc mặt phẳng $(O x y)$ sao cho $|\overrightarrow{M A}+\overrightarrow{M B}+2 \overrightarrow{M C}|$ đạt giá trị nhỏ nhất. Toa độ của điểm $M$ là
Câu số 43:
Gọi $S$ là tập hợp tất cả các giá trị thực của tham số m để đồ thị của hàm số $y=$ $\frac{x^{2}+m x+2 m}{x+1}$ có hai điểm cực trị $A, B$ và tam giác $O A B$ vuông tại O. Tổng tất cả các phần tử của $S$ bằng
Câu số 44:
Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại C, AB = 2a và góc tạo bởi hai mặt phằng $\left(A B C^{\prime}\right)$ và $(A B C)$ bàng $60^{\circ}$. Goi $M, N$ lần lượt là trung điểm của $A^{\prime} C^{\prime}$ và $B C .$ Măt phằng $(A M N)$ chia khôi lăng trụ thành hai phần. Thể tích của phần nhỏ bằng
Câu số 45:
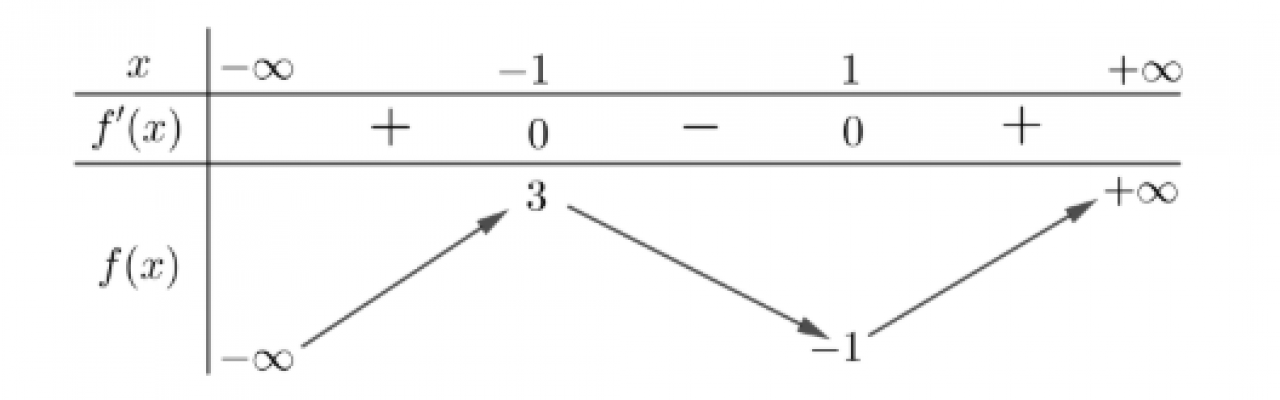
Cho hàm số $f(x)$ có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của tham số m để phương trình $f(\sqrt{x-1}-1)+x+3-4 \sqrt{x-1}=m$ có hai nghiệm phân biệt ?
Câu số 46:
Cho hàm số $f(x)$ có đạo hàm trên khoảng $(0 ;+\infty)$ thỏa mãn $f(x)=x\left[\sin x+f^{\prime}(x)\right]+\cos x$ và $f\left(\frac{\pi}{2}\right)=\frac{\pi}{2} .$ Giá trị của $f(\pi)$ bằng
Câu số 47:
Xét các số phức thỏa mãn |z|\geq 2. Gọi M và m là giá trị lớn nhất và giá trị nhỏ nhất của $\left|\frac{z+i}{z}\right| .$ Giá trị của tích $M m$ bằng
Câu số 48:
Cho hàm số $y=x^{3}-3 x+1$ có đồ thị (C). Xét các điểm $A, B$ thay đổi thuộc (C) sao cho tiếp tuyến của (C) tại A, B song song với nhau. Gọi E, F lần lượt là giao điểm của các tiếp tuyến tại $A$ và $B$ với trục tung. Có bao nhiêu điểm $A$ có hoành độ là số nguyên dương sao cho $E F<2020$ $?$
Câu số 49:
Trong không gian Oxyz, cho mặt cầu (S) : $x^{2}+y^{2}+z^{2}-2 x-4 y+6 z-13=0$ và đường thẳng $d: \frac{x+1}{1}=\frac{y+2}{1}=\frac{z-1}{1} .$ Lấy điểm $M(a ; b ; c)$ với $a<0$ thuộc đường thẳng $d$ sao cho từ $M$ kẻ được ba tiếp tuyến $M A, M B, M C$ đến mặt cầu $(S)(A, B, C$ là các tiếp điểm) thỏa mãn $\widehat{A M B}=60^{\circ}, \widehat{B M C}=90^{\circ}, \widehat{C M A}=120^{\circ}$. Tổng $a+b+c$ bằng
Câu số 50:
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ và thỏa mãn $f^{3}(x)+2 f(x)=1-x$ với mọi $x \in \mathbb{R}$. Tích phân $\int^{1}_{-2} f(x) \mathrm{d} x$ bằng
