Câu số 1:  

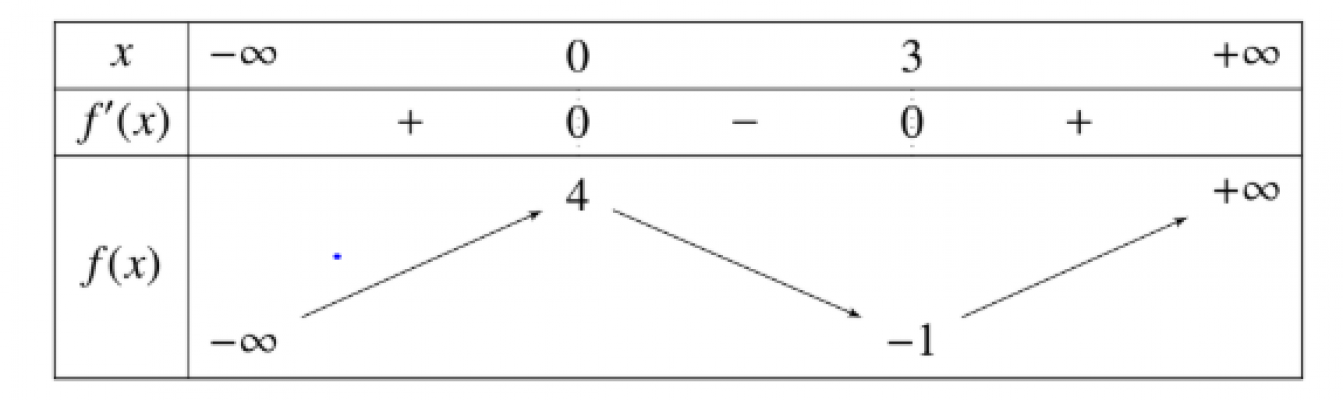
Cho hàm số $y = f(x)$ có bảng biến thiên như sau. Mệnh đề nào sau đây đúng?

Câu số 2:  

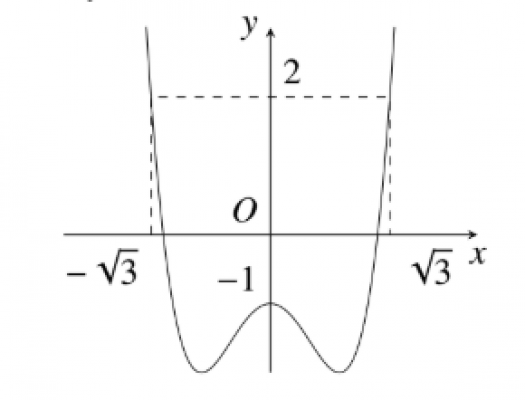
Đường cong trong hình vẽ bên là của hàm số nào trong 4 hàm số dưới đây?

Câu số 3:  

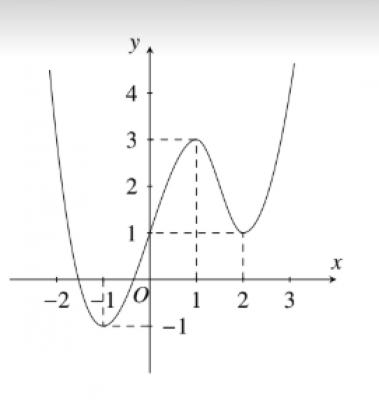
Cho đồ thị của hàm số y $=f(x)$ như hình vẽ. Tìm số giá trị nguyên của $m$ để phương trình $f(x)=m$ có đúng 3 nghiệm phân biệt

Câu số 4:  

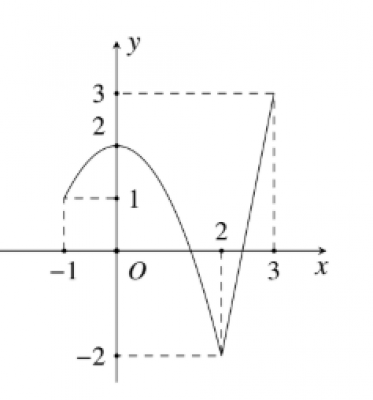
Cho hàm số $y=f(x)$ liên tục trên đoạn $[-1 ; 3]$ có đồ thị như hình vẽ bên. Gọi $M$ và $m$ làn lượt là giá trị lớn nhất, giá trị nhở nhất của hàm số đã cho trên đoạn $[-1 ; 3] .$ Giá trị của $M-m$ bằng

Câu số 5:  

Cho khối trụ (T) có bán kính đáy bằng 4 và diện tích xung quanh bằng 16 trụ (T).

Câu số 6:  

Giá trị của biểu thức $M=\log _{2} 2+\log _{2} 4+\log _{2} 8+\ldots+\log _{2} 256$ bằng

Câu số 7:  

Tiệm cận ngang của đồ thị hàm số y $=\frac{3 x+2}{x+1}$ là

Câu số 8:  

Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A (1; 1; -2) và B (2; 2; 1). Véc tơ $\overrightarrow{AB}$ có tọa độ là

Câu số 9:  

Trong không gian với hệ trục tọa độ Oxyz, cho véc tơ $\vec{a}=(1 ;-2 ; 3) .$ Tim tọa độ của véc tơ $\vec{b}$ biết rằng véc tơ $\vec{b}$ ngược hướng với véc tơ $\vec{a}$ và $|\vec{b}|=2|\vec{a}|$

Câu số 10:  

Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm $M(1 ; 2 ;-4)$ và $M^{\prime}(5 ; 4 ; 2) .$ Biết rằng $M^{\prime}$ là hình chiếu vuông góc của M lên mặt phắng ( $\alpha$ ), khi đó mặt phẳng ( $\alpha$ ) có một véc tơ pháp tuyến là