Câu số 1:   Cho hàm số $y=\sqrt[4]{x^2-3}$, phương trình $y'=0$ có mấy nghiệm thực:

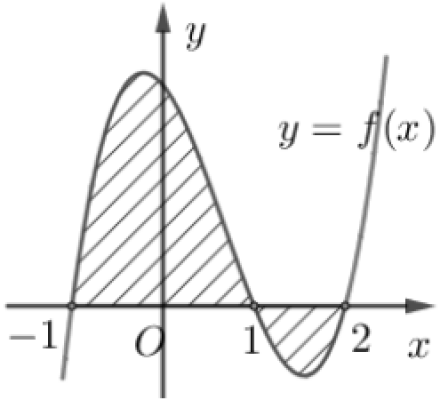
Câu số 2:   Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$. Gọi $S$ là diện tích hình phẳng giới hạn bởi các đường $y=f(x), y=0,x=-1$ và $x=2$ (như hình vẽ bên). Mệnh đề nào dưới đây là đúng?

Câu số 3:   Hàm số $y=x^4-4x^2+3$ đồng biến trên khoảng nào trong những khoảng đã cho sau?

Câu số 4:   Phương trình $2^{2x+1}=32$ có nghiệm là

Câu số 5:   Cho hàm số $y=\frac 1 4 x^4 - \frac 7 2 x^2$ có đồ thị $(C)$. Có bao nhiêu điểm $A$ thuộc $(C)$ sao cho tiếp tuyến của $(𝐶)$ tại $𝐴$ cắt $(𝐶)$ tại hai điểm phân biệt $M(x_1;y_1),N(x_2;y_2)$ ($M,N$ khác $A$) thỏa mãn $y_1-y_2=6(x_1-x_2)$)?

Câu số 6:   Cho phương trình $5^x + 𝑚 = \log^5 (𝑥 − 𝑚)$ với $m$ là tham số. Có bao nhiêu giá trị nguyên của $𝑚 \in (−20; 20)$ để phương trình đã cho có nghiệm ?

Câu số 7:   Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y= x^3+ x^2+ mx+1$ đồng biến trên $(-\infty;+\infty)$

Câu số 8:   Giá trị lớn nhất của hàm số $f(x)=x^3-3x$ trên đoạn [-3;3] bằng

Câu số 9:   Nghiệm của phương trình $\log_2(x+1)+1 = \log_2(3x-1)$ là

Câu số 10:   Cho hàm số $y=\frac{x^2-1}{x}$. Khẳng định nào sau đây là khẳng định đúng.