Câu số 1:  

Cho số phức z thỏa mãn $11z^{2018} + 10iz^{2017} + 10iz - 11 = 0$ . Mệnh đề nào sau đây đúng?

Câu số 2:  

Cho các số phức $z_{1} = -3i$, $z_{2} = 4 + i$ và z thỏa mãn $\left | z - i \right | = 2$. Biết biểu thức $T = \left | z - z_{1} \right |+2\left | z - z_{2} \right |$ đạt giá trị nhỏ nhất khi z = a + bi, $(a,b\in \mathbb{R})$. Hiệu a - b bằng:

Câu số 3:  

Cho số phức z Gọi A, B lần lượt là các điểm trong mặt phẳng Oxy biểu diễn các số phức (1 + i)z Tính $\left | z \right |$ biết diện tích tam giác OAB bằng 8.

Câu số 4:  

Cho các số phức w,z thỏa mãn $\left | w + i \right |= \frac{3\sqrt{5} }{5}$ và 5w = (2 + i)(z - 4). Giá trị lớn nhất của biểu thức $P = \left | z - 1 - 2i \right |+ \left |z - 5 - 2i \right |$ bằng

Câu số 5:  

Cho số phức z thỏa mãn $\left | z-4 \right | + \left | z + 4 \right | = 10$. Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của $\left | z \right |$ . Tính M + m

Câu số 6:  

Cho số phức thỏa mãn $\left | z - 1 \right | = \left | z - 2 + 3i \right |$. Tập hợp các điểm biểu diện số phức z là

Câu số 7:  

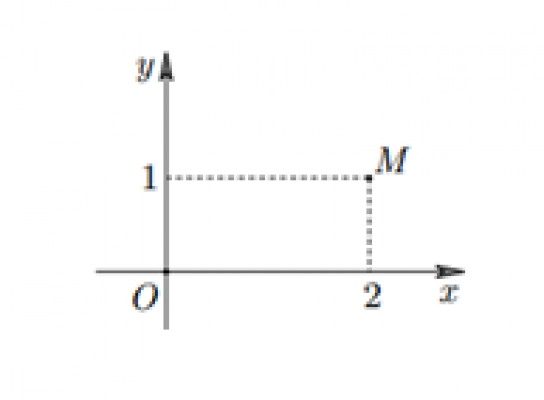
Trong hình vẽ bên, điểm M biểu diễn số phức z. Số phức $\bar{z}$ là:

Câu số 8:  

Cho số phức z thỏa mãn $\left | z \right |-2\bar{z} = -7 + 3i+z$. Tính $\left | z \right |$

Câu số 9:  

Có bao nhiêu số phức z thỏa mãn (1+i)z + (1-i)$ \bar{z}$ = 13 + 2i

Câu số 10:  

Gọi A,B,C lần lượt là các điểm biểu siễn các số phức $z_{1}=2$, $z_{2}=4i$, $z_{3}=2+4i$. Tính diện tích tam giác ABC