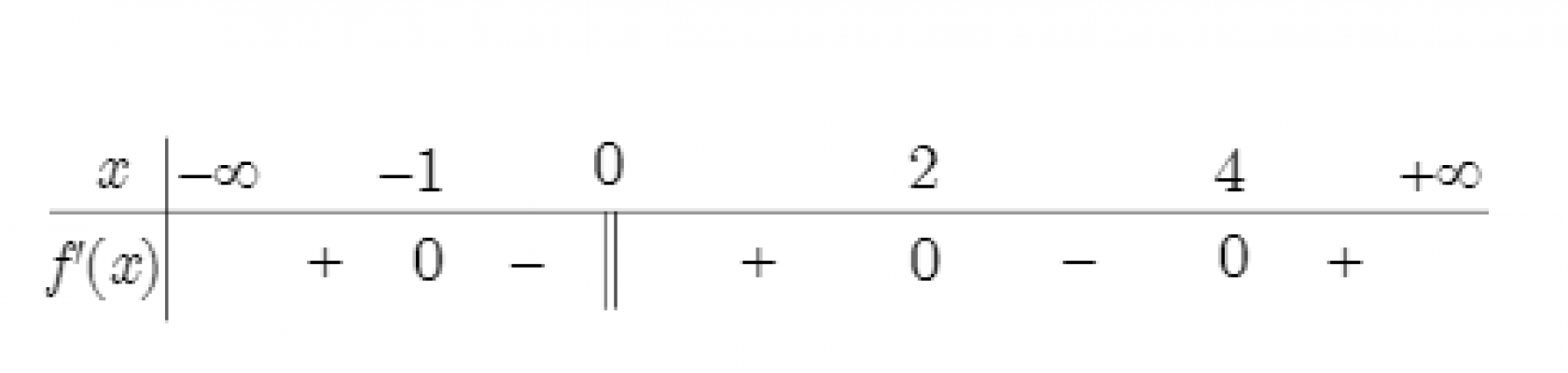Câu số 1:
Cho số phức $z = a + bi$ với $a,b$ là các số thực bất kỳ. Mệnh đề nào sau đây đúng?
Câu số 2:
Giả sử $F(x)$ là một nguyên hàm của hàm số $f(x) = \frac{1}{3x + 1}$ trên khoảng $\left ( -\infty ; -\frac{1}{3}\right )$. Mệnh đề nào sau đây đúng?
Câu số 3:
Cho tứ diện $OABC$ có $OA, OB, OC$ đôi một vuông góc với nhau và $OA = a, OB= 2a, OC = 3a$. Thể tích của khối tứ diện $OABC$ bằng
Câu số 4:
Cho hàm số $y = f(x)$ có đạo hàm ${f}'(x) = x(x-2)^{3}$ với mọi $x \in R$. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Câu số 5:
Cắt một hình trụ bằng một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông cạnh $2a$. Diện tích xung quanh của hình trụ bằng
Câu số 6:
Trong không gian $Oxyz$ cho điểm $M(1; 1; 2)$ và mặt phẳng $(P): 2x - y + 3z + 1 = 0$. Đường thẳng đi qua điểm $M$ và vuông góc với mặt phẳng $(P)$ có phương trình là
Câu số 7:
Một nhóm học sinh có 10 người. Cần chọn 3 học sinh trong nhóm để làm 3 công việc là tưới cây, lau bàn và nhặt rác, mỗi người làm một công việc. Số cách chọn là
Câu số 8:
Cho $\log_{a}c = x > 0$ và $\log_{b}c = y > 0$. Khi đó giá trị của $\log_{ab}c$ là
Câu số 9:
Giá trị của $\lim_{x\rightarrow -\infty }\frac{2x -1}{\sqrt{x^{2} +1} - 1}$ bằng
Câu số 10:
Cho hàm số $y = f(x)$ liên tục trên R và có bảng xét dấu của đạo hàm như hình vẽ. Hàm số đã cho có bao nhiêu điểm cực trị