Câu số 21:  

Trong các hàm số sau, hàm số nào đồng biến trên tập xác định của nó?

Câu số 22:  

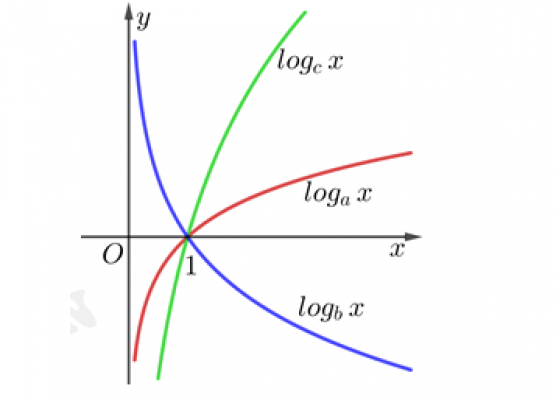
Cho a,b,c là các số thực dương và khác 1. Hình vẽ bên là đồ thị của ba hàm số $y = log_{a}x, y = log_{b}x ; y = log_{c}x$. Khẳng định nào sau đây là đúng?

Câu số 23:  

Trong không gian với hệ tọa độ Oxyz, cho ba điểm M(0;1;0); N(0;0;2); A(3;2;1). Lập phương trình mặt phẳng (MNP), biết điểm P là hình chiếu vuông góc của điểm A trên trục Ox.

Câu số 24:  

Tìm giá trị của tham số m để hàm số $y = \frac{1}{3}x^{3}- mx^{2} +(m^{2} - m + 1)x + 1$ đạt cực đại tại x = 1?

Câu số 25:  

Tính giới hạn $I = \lim_{x\rightarrow -\infty }\frac{5x - 2}{3x +1}$

Câu số 26:  

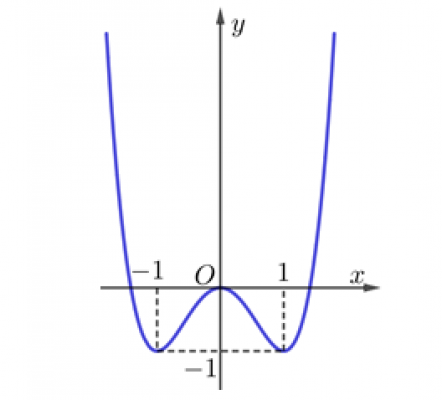
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A,B,C,D dưới đây. Hỏi hàm số đó là hàm số nào?

Câu số 27:  

Trong không gian với hệ tọa độ Oxyz, tính bán kính R của mặt cầu (S): $x^{2}+y^{2}+z^{2} - 2x - 2y = 0$

Câu số 28:  

Cho hình trụ bán kính đáy r = 5 (cm) và khoảng cách giữa hai đáy bằng 8 (cm). Diện tích xung quanh của hình trụ là:

Câu số 29:  

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): $(x -1)^{2}+(y +1^{2}) +z^{2} = 8$ và hai đường thẳng $d_{1}: \frac{x + 1}{1} = \frac{y - 1}{1} = \frac{z - 1}{2}$ ; $d_{2}: \frac{x + 1}{1} = \frac{y}{1}=\frac{z}{1}$. Viết phương trình tất cả các mặt phẳng tiếp xúc với mặt cầu (S) đồng thời song song với hai đường thẳng $d_{1}$, $d_{2}$

Câu số 30:  

Tích phân bằng $I = \int_{0}^{\frac{\pi }{3} }\sin xdx$