Câu số 31:  

Cho hàm số $y = x(x^{2}-3)$ có đồ thị (C). Có bao nhiêu điểm M thuộc đồ thị (C) thỏa mãn tiếp tuyến tại M của (C) cắt (C) và trục hoành lần lượt tại hai điểm phân biệt A (khác M) và B sao cho M là trung điểm của đoạn thẳng AB?

Câu số 32:  

Tập hợp nào sau đây chứa tất cả các giá tị của tham số m sao cho giá trị lớn nhất của hàm số $y = \left | x^{2} -2x +m\right |$ trên đoạn [-1;2] bằng 5?

Câu số 33:  

Cho $\int_{\frac{1}{3} }^{1}\frac{x}{3x+\sqrt{9x^{2}-1} } = a+b\sqrt{2}$ với a,b là các số hữu tỉ. Khi đó giá trị của a là:

Câu số 34:  

Cho hình chóp đa giác đều có các cạnh bên bằng a và tạo với mặt đấy của hình chóp một góc $30^{\circ}$. Tính thể tích khối cầu ngoại tiếp của hình chóp

Câu số 35:  

Cho số phức z thỏa mãn $\left | z \right |-2\bar{z} = -7 + 3i+z$. Tính $\left | z \right |$

Câu số 36:  

Cho hàm số f(x) xác định trên $\mathbb{R}\setminus \left \{ -1;1 \right \}$ và thỏa mãn $f'(x) = \frac{1}{x^{2}-1}; f(-3)+f(3) = 0$ và $f(-\frac{1}{2})+f(\frac{1}{2})=2$. Tính giá tị của biểu thức P = f(0) + f(4).

Câu số 37:  

Cho phương trình $log_{0,5}(m+6x)+log_{2}(3-2x-x^{2})$ (m là tham số). Có bao nhiêu giá trị nguyên dương của m để phương trình có nghiệm thực?

Câu số 38:  

Cho hàm số y = f(x) có đúng ba điểm cực trị là -2;-1;0 và có đạo hàm liên tục trên $\mathbb{R}$. Khi đó hàm số $y = f(x^{2}-2x)$ có bao nhiêu điểm cực trị?

Câu số 39:  

Có bao nhiêu giá trị nguyên hàm của tham số m nhỏ hơn 10 để phương trình sau $\sqrt{m+\sqrt{m+e^{2} } } = e^{x}$ có nghiệm thực?

Câu số 40:  

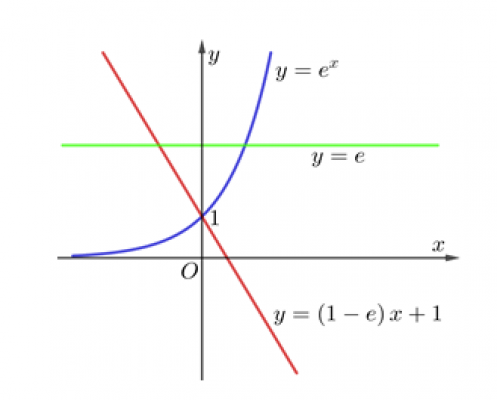
Cho (H) là hình phẳng giới hạn bởi các đồ thị hàm số y = e, $y = e^{x}$ và y = (1-e)x +1 (tham khảo hình dưới đây). Diện tích của (H) là