Câu số 31:  

Cho hàm số $y=f(x)$ liên tục trên $R$ và có đồ thị như hình bên. Số nghiệm phân biệt của phương trình $f(f(x))=-2$ là

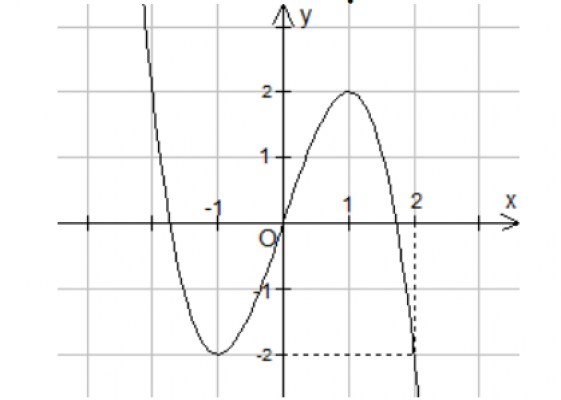
Câu số 32:  

Cho tam giác ABC có BC=a, CA =b, AB=c. Nếu a, b, c theo thứ tự lập thành một cập số nhân thì

Câu số 33:  

Có bao nhiêu sổ nguyên $x$ nghiệm đúng bất phương trình $\frac{1}{\log _{x} 2}+\frac{1}{\log _{x^{2} } 2}<5 ?$

Câu số 34:  

Xét các khẳng định sau:

i)Nếu hàm số y=f(x) có đạo hàm cấp hai trên $R$ và đạt cực tiểu tại $x = x_{0}$ thì  $\left\{\begin{array}{l}{f}^{\prime}({x}_{0})=0 \newline {f}^{\prime\prime}({x}_{0})>0 \end{array}\right.$

ii)Nếu hàm số y=f(x) có đạo hàm cấp hai trên $R$ và đạt cực đại tại $x = x_{0}$ thì $\left\{\begin{array}{l}{f}^{\prime}({x}_{0})=0 \newline {f}^{\prime\prime}({x}_{0})<0 \end{array}\right.$

iii) Nếu hàm số y=f(x) có đạo hàm cấp hai trên $R$ và ${f}^{\prime\prime}(x_{0}) = 0$ thì hàm số không đạt cực trị tại $x = x_{0}$

Số khẳng định đúng trong các khẳng định trên là

Câu số 35:  

Một chất điểm chuyển động trên trục Ox với tốc độ thay đổi theo thời gian v = f(t) (m/s). Quãng đường chất điểm đó chuyển động trên trục Ox từ thời điểm $t_{1}$ đến thời điểm $t_{2}$ là ${s}=\int_{ {t}_{1} }^{ {t}_{2} }{f}({t}) {d} {t}$. Biết rằng v(t) = 30 - 5t (m/s), quãng đường chất điểm đó đi được từ thời điểm $t_{1}= 1s$ đến thời điểm ${t}_{2}=2 {s}$ bằng bao nhiêu mét?

Câu số 36:  

Cho các hàm số y=f(x) và y=g(x) liên tục trên $R$ thỏa mãn f(x)> g(x) > 0 với mọi số thực x. Thể tích khối tròn xoay khi quay hình phẳng D trong hình vẽ xung quanh trục Ox được tính bởi công thức:

Câu số 37:  

Xét các khẳng định sau

i) $\left|z_{1}-z_{2}\right|^{2}=\left(z_{1}-z_{2}\right)^{2} \forall z_{1}, z_{2} \in \mathbb{C}$

ii) $\left|z_{1}-z_{2}\right|^{2}=\left(z_{1}-z_{2}\right) \overline{\left(z_{1}-z_{2}\right)} \forall z_{1}, z_{2} \in \mathbb{C}$

iii) $\left|z_{1}\right|^{2}+\left|z_{2}\right|^{2}=2\left|\frac{z_{1}+z_{2} }{2}\right|^{2}+\frac{1}{2}\left|z_{1}-z_{2}\right|^{2} \forall z_{1}, z_{2} \in \mathbb{C}$

Số khẳng định đúng là

Câu số 38:  

Cho hình thang cân $ABCD, AB// CD, AB=6 cm, {CD}=2cm$ $AD=BC=\sqrt{13} cm .$ Quay hinh thang $ABCD$ xung quanh đường thẳng $AB$ ta được một khối tròn xoay có thể tích là

Câu số 39:  

Trong không gian tọa độ Oxyz, cho hai điểmA(1; 0;0), B(5;0;0). Gọi $(H)$ là tập hợp các điểm M trong không gian thỏa mãn $\overrightarrow{MA}$.$\overrightarrow{MB}$ = 0. Khẳng định nào sau đây là đúng?

Câu số 40:  

Cho khối chóp S.ABC có $(SAB)\perp (ABC), (SAC)$ $\perp(\mathrm{ABC}), \mathrm{SA}=\mathrm{a}, \mathrm{AB}=\mathrm{AC}=2 \mathrm{a}$,  $\mathrm{BC}=2 \mathrm{a} \sqrt{2} $ Gọi M là trung điểm của BC. Khoảng cách giữa hai đường thắng SM và AC bằng