Câu số 41:
Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có bảng xét dấu của đạo hàm như sau. Có bao nhiêu giá trị nguyên của tham số $m$ để hàm số $g(x)=f(x+m)$ đồng biến trên khoảng $(0 ; 2)$

Câu số 42:
Cho $A(1 ; 4 ; 2), B(-1 ; 2 ; 4)$, đường thẳng $d:\left\{\begin{array}{l}x=5-4 t \\ y=2+2 t \\ z=4+t\end{array}\right.$ và điểm $M $ thuộc $d$ giá trị. Tìm giá trị nhỏ nhất của diện tích tam giác $AMB$
Câu số 43:
Cho phương trình $\log _{3}^{2} x-4 \log _{3} x+m-3=0$. Tìm tất cả cả giá trị nguyên của tham số m để phương trình đã cho có hai nghiệm phân biệt $x_{1}<x_{2}$ thỏa mãn $x_{2}-81 x_{1}<0$
Câu số 44:
Cho hai số phức $z_{1}, z_{2}$ khác 0 thỏa mãn $\frac{z_{1} }{z_{2} }$ là số thuần ảo và $\left|z_{1}-z_{2}\right|=10 .$ Giá trị lớn nhất của | $z_{1}|+| z_{2} |$ bằng
Câu số 45:
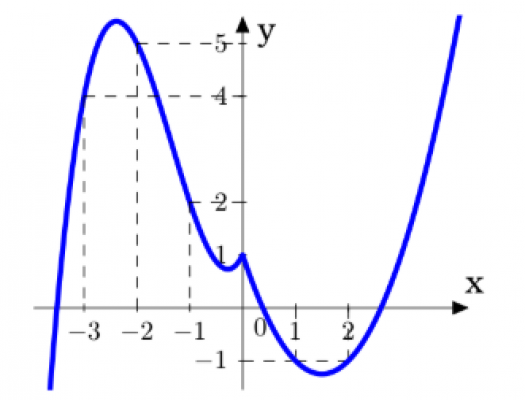
Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ có đồ thị như hình vẽ. Biết trên $(-\infty ;-3) \cup(2 ;+\infty)$ thì $f^{\prime}(x)>0 .$ Số nghiệm nguyên thuộc (-10;10) của bất phương trình $[f(x)+x-1]\left(x^{2}-x-6\right)>0$ là
Câu số 46:
Cho hình chóp $S . A B C$ có đáy $A B C$ là tam giác vuông cân tại $A,$ hình chiếu vuông góc của đỉnh $S$ trên mặt phẳng ( $A B C$ ) là một điểm nằm trên đoạn thẳng $B C$. Mặt phẳng $(S A B)$ tạo với $(S B C)$ một góc $60^{0}$ và mặt phẳng $(S A C)$ tao với $(S B C)$ một góc $\varphi$ thỏa mãn $\cos \varphi=\frac{\sqrt{2} }{4} $. Gọi $\alpha$ là góc tạo bởi $S A$ và mặt phẳng $(A B C),$ tính tan$\alpha$
Câu số 47:
Cho hàm số $y=f(x)$ có đồ thị (C), biết tiếp tuyến của đồ thị (C) tại điểm có hoành độ $x=0$ là đường thẳng $y=3 x-3 .$ Giá trị của $\lim _{x \rightarrow 0} \frac{3 x}{f(3 x)-5 f(4 x)+4 f(7 x)}$ là
Câu số 48:
Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ sao cho $\max _{x \in[0 ; 10]} f(x)=f(2)=4 .$ Xét hàm só $g(x)=f\left(x^{3}+x\right)-x^{2}+2 x+m .$ Giá trịcủa tham số $m$ đề $\max _{x \in[0 ; 2]} g(x)=8$ là
Câu số 49:
Cho đa thức bậc bốn $y=f(x)$ đạt cực trị tại $x=1$ và $x=2$. Biết $\lim _{x \rightarrow 0} \frac{2 x+f^{\prime}(x)}{2 x}=2$.Tich phân $\int_{0}^{1} f^{\prime}(x) d x$ bằng
Câu số 50:
Cho hàm số $f(x)=x^{5}+3 x^{3}-4 m$. Có bao nhiêu giá trị nguyên của tham số $m$ để phương trình $f(\sqrt[3]{f(x)+m})=x^{3}-m$ có nghiệm thuộc $[1 ; 2] ?$
