Câu số 31:  

Số nghiệm thực của phương trình $\log_{3}(x)+\log _{3}(x-6)=\log _{3} 7$ là

Câu số 32:  

Cho bốn điểm $A, B, C, D$ trên hình vẽ biểu diễn 4 số phức khác nhau. Chọn mệnh đề sai.

Câu số 33:  

Đường cong trong hình bên là đồ thị của một trong bốn hàm số được liệt kê ở bốn phương án $A, B, C, D$ dưới đây. Hỏi hàm số đó là hàm số nào?

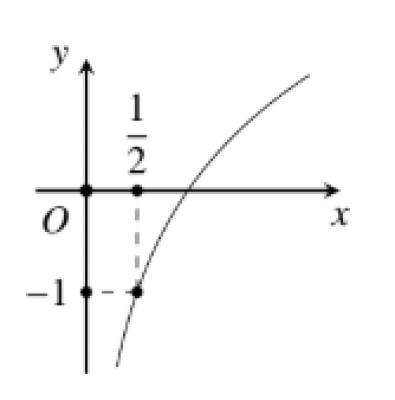
Câu số 34:  

Trong không gian với hệ tọa độ Oxyz, cho hình bình hành ABCD với A (-2; 3; 1), B (3; 0; -1), C (6; 5; 0). Tọa độ đỉnh D là

Câu số 35:  

Cho hàm số $y=f(x)$ có đạo hàm trên $\mathbb{R}$. Đồ thị hàm số $y=f^{\prime}(x)$ như hình vẽ. Hàm số $y=f\left(x^{2}+2 x\right)$ đồng biến trên khoảng nào sau đây?

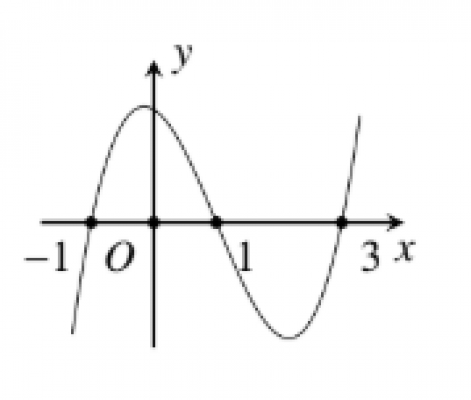
Câu số 36:  

Cho hàm số $y=f(x)$ có đạo hàm trên $\mathbb{R}$ và có đồ thị như hình vẽ. Hàm số $y=$ $f\left(x^{2}-2 x\right)$ có bao nhiêu điểm cực trị?

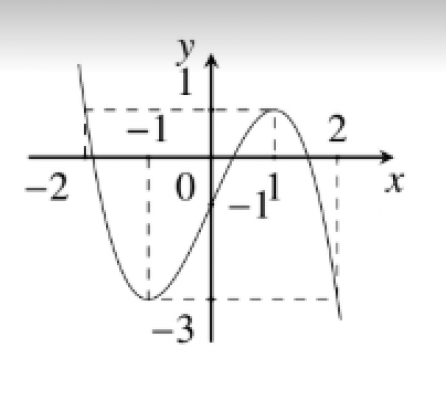
Câu số 37:  

Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ. Hàm số $y=|f(x)|$ có bao nhiêu cực trị?

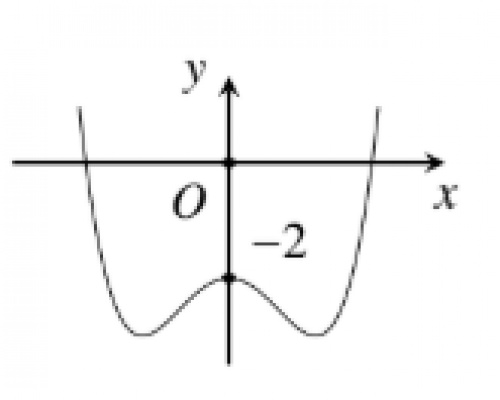
Câu số 38:  

Cho phương trình $\log _{2}(x-1)=\log _{2}(x-2) m$. Tất cả các giá trị của $m$ để phương trình trên có nghiệm là

Câu số 39:  

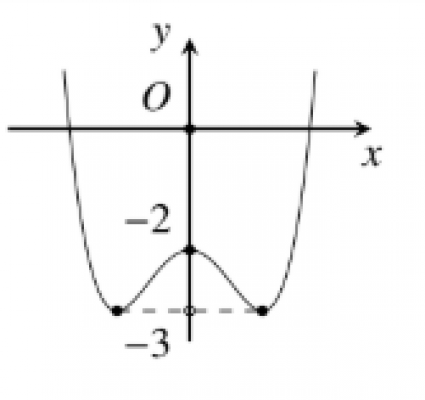
Đường cong trong hình vẽ là đồ thị hàm số $y=x^{4}-2 x^{2}-2 .$ Tìm $m$ để phương trình $x^{4}-2 x^{2}=m$ có bốn nghiệm phân biệt.

Câu số 40:  

Cho $\log _{2} 6=a .$ Khi đó giá trị của log $_{3} 18$ được tính theo $a$ là