Câu số 41:  

Cho $z \in \mathbb{C},|z-2+3 i|=5 .$ Biết rằng tập hợp biểu diễn số phức $ w=i . \bar{z}+12-i$ là một đường tròn có bán kính $R$. Bán kính $R$ là

Câu số 42:  

Tìm tất cả các giá trị thực của $m$ để đường thẳng $y=m x-m$ cắt đồ thị hàm số $y=x^{3}-3 x^{2}+2$ tại ba điểm phân biệt $A, B, C$ sao cho $A B=B C$.

Câu số 43:  

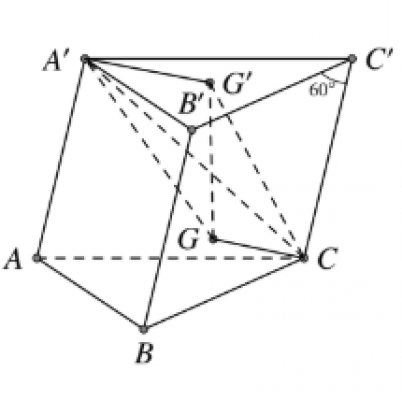
Cho hình lăng trụ $A B C . A^{\prime} B^{\prime} C^{\prime}$ có thể tích $V .$ Biết tam giác $A B C$ là tam giác đều cạnh $a$, các mặt bên là hình thoi, $\widehat{C C^{\prime} B^{\prime} }=60^{\circ} .$ Gọi $G, G^{\prime}$ lần lượt là trọng tâm của tam giác $B C B^{\prime}$ và tam giác $A^{\prime} B^{\prime} C^{\prime} .$ Tính theo $V$ thể tích của khối đa diện $G G^{\prime} C A^{\prime}$

Câu số 44:  

Cho phương trình 2 $^{2 x}-5.2^{x}+6=0$ có hai nghiệm $x_{1}, x_{2} .$ Tính $P=x_{1} . x_{2}$

Câu số 45:  

Cho $z \in \mathbb{C}$ thỏa mãn $|\bar{z}+2 i| \leq|z-4 i|$ và $(z-3-3 i)(\bar{z}-3+3 i)=1 .$ Giá trị lớn nhất của biểu thức $|z-2|$ là

Câu số 46:  

Cho số phức $z = a + bi$ ( $a, b \in \mathbb{R}$ ) thỏa mãn $|z| = 5 $ và $(4 - 3 i) z$ là một số thực. Giá trị $|a| + |b|+3$ là

Câu số 47:  

Trong không gian với hệ trục tọa độ Oxyz, cho ba mặt phẳng (P): $x+y+z+5=0 ;(Q): x+y+z+1=0$ và $(R): x+y+z+2=0 .$ Ứg với mỗi cặp $A, B$ lần lượt thuộc hai mặt phẳng ( $P$ ) và ( $Q$ ) thì mặt cầu đường kính $A B$ luôn cắt mặt phẳng (R) tạo thành một đường tròn. Tìm bán kính nhỏ nhất của đường tròn đó.

Câu số 48:  

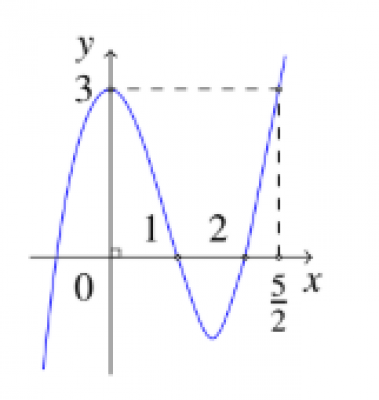
Cho $y=f(x)$ có đồ thị như hình vẽ. Định $m$ để bất phương trình dưới đây đúng $\forall x \geq 1$

$\log _{2}[f(x+m)+1]<\log _{\sqrt{3} } f(x+m)$

Câu số 49:  

Tìm tất cả giá trị m để phương trình ( $m-1$ ) $\log _{\frac{1}{2} }^{2}(x-2)-(m-5) \log _{\frac{1}{2} }(x-2)+m-1=0$ có đúng hai nghiệm thực thuộc (2; 4).

Câu số 50:  

Có bao nhiêu số nguyên x nghiệm đúng bất phương trình $\frac{1}{\log _{x} 2}+\frac{1}{\log _{x^{+} } 2}<10 ?$