Câu số 1: Có bao nhiêu cách chọn hai học sinh từ một nhóm gồm 34 học sinh?
Câu số 2: Trong không gian $𝑂𝑥𝑦𝑧$, mặt phẳng $(𝑃):𝑥 + 2𝑦 + 3𝑧 − 5 = 0$ có một vectơ pháp tuyến là
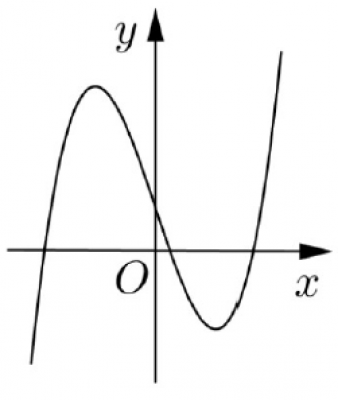
Câu số 3: Cho hàm số $y = ax^3 + bx^2 + cx + d$ $(a,b,c,d \in \mathbb{R})$ có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là
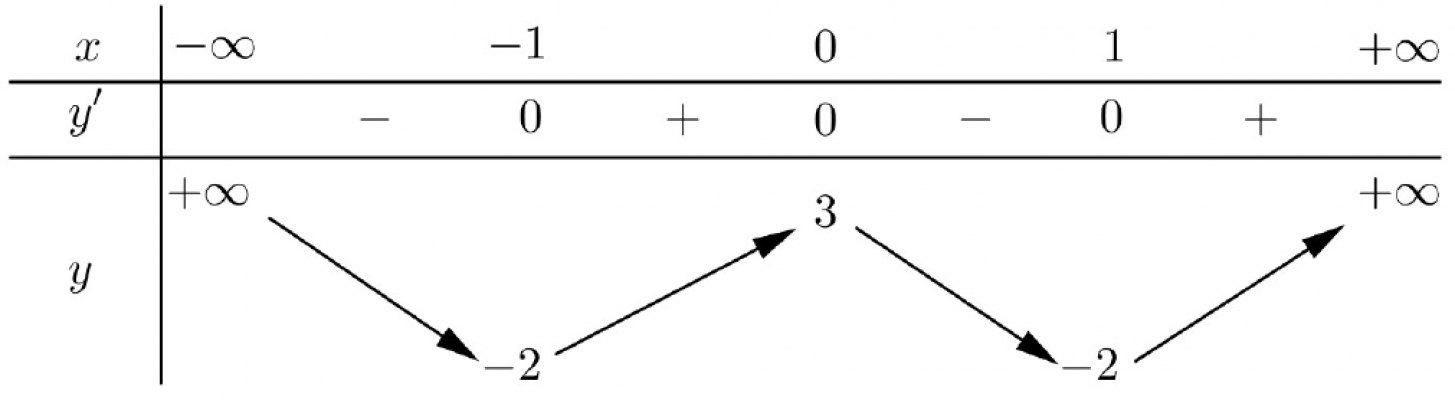
Câu số 4: Cho hàm số $y=f(x)$ có bảng biến thiên như sau. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Câu số 5: Gọi $S$ là diện tích của hình phẳng giới hạn bởi các đường $y=e^x, y=0, x=0, x=2$. Mệnh đề nào dưới đây đúng?
Câu số 6: Với $a$ là số thực dương tùy ý, $\ln(5𝑎) − \ln(3𝑎)$ bằng
Câu số 7: Nguyên hàm của hàm số $f(x)=x^3+x$ là
Câu số 8: Trong không gian $𝑂𝑥𝑦𝑧$, đường thẳng $$\left\{\begin{array}{l} x=2-t \newline y=1+2t \newline x=3+t \end{array}\right.$$ có một vectơ chỉ phương là
Câu số 9: Số phức $−3 + 7i$ có phần ảo bằng
Câu số 10: Diện tích của mặt cầu bán kính $𝑅$ bằng
-

phương - 10 tháng trước
h
